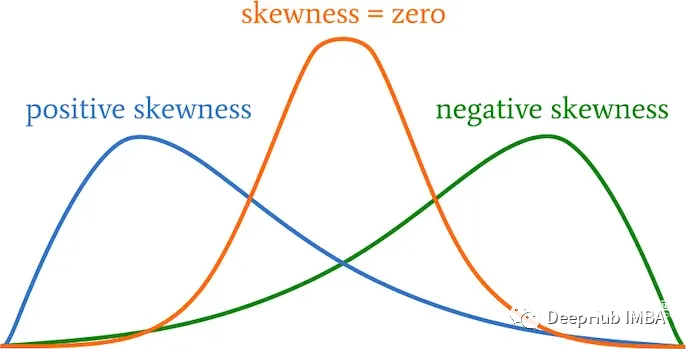
偏度(skewness)是用來(lái)衡量概率分布或數(shù)據(jù)集中不對(duì)稱(chēng)程度的統(tǒng)計(jì)量。它描述了數(shù)據(jù)分布的尾部(tail)在平均值的哪一側(cè)更重或更長(zhǎng)。偏度可以幫助我們了解數(shù)據(jù)的偏斜性質(zhì),即數(shù)據(jù)相對(duì)于平均值的分布情況。
有時(shí),正態(tài)分布傾向于向一邊傾斜。這是因?yàn)閿?shù)據(jù)大于或小于平均值的概率更高,因此使得分布不對(duì)稱(chēng)。這也意味著數(shù)據(jù)不是均勻分布的。
偏度可以與其他描述性統(tǒng)計(jì)一起描述變量的分布。通過(guò)偏度也可以判斷變量是否為正態(tài)分布。因?yàn)檎龖B(tài)分布的偏度為零,是許多統(tǒng)計(jì)過(guò)程的假設(shè)。
偏度分類(lèi)
分布可以有右偏度(或正偏度)、左偏度(或負(fù)偏度)或零偏度。右偏態(tài)分布在其峰值的右側(cè)較長(zhǎng),而左偏態(tài)分布在其峰值的左側(cè)較長(zhǎng)。
1、零偏度
—當(dāng)一個(gè)分布的偏度為零時(shí),它是對(duì)稱(chēng)的。它的左右兩邊是鏡像。正態(tài)分布的偏度為零,但不是只有正態(tài)分布的偏度為零。任何對(duì)稱(chēng)分布,如均勻分布或某些雙峰分布,偏度都是零。
檢查變量是否具有傾斜分布的最簡(jiǎn)單方法是將其繪制成直方圖。

分布近似對(duì)稱(chēng),觀測(cè)值在峰值的左右兩側(cè)分布相似。因此分布的偏度近似為零。
在零偏度的分布中,平均值和中位數(shù)是相等的,也就是說(shuō):
mean = median
2、右偏(正偏)
右偏分布在其峰值的右側(cè)比其左側(cè)更長(zhǎng)。右偏也被稱(chēng)為正偏。它表明在分布的極端一端有觀測(cè)值,但它們相對(duì)較少。右偏分布的右側(cè)有一條長(zhǎng)尾。
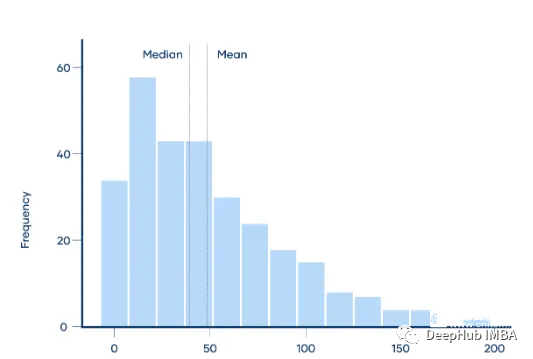
分布是右偏的,因?yàn)樗诜逯涤覀?cè)的時(shí)間更長(zhǎng)。右偏分布的均值幾乎總是大于中位數(shù)。這是因?yàn)闃O值(尾部的值)對(duì)均值的影響大于中位數(shù)。
mean > median
3、左偏(負(fù)偏)
左偏分布的峰值左側(cè)比右側(cè)更長(zhǎng)。左偏分布的左側(cè)有一條長(zhǎng)尾。左偏也被稱(chēng)為負(fù)偏。
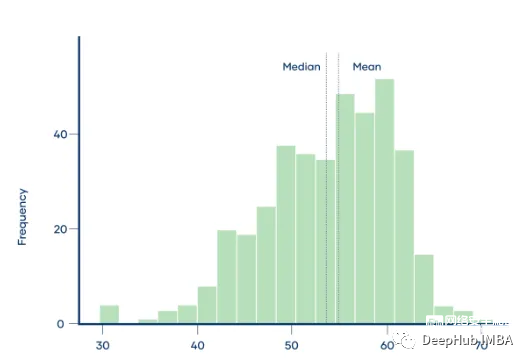
這個(gè)分布是左偏的,因?yàn)樗诜逯档淖髠?cè)更長(zhǎng)。左偏分布的均值幾乎總是小于中位數(shù)。
mean < median
偏度計(jì)算
有幾個(gè)公式可以用來(lái)測(cè)量偏度。其中最簡(jiǎn)單的是皮爾遜中值偏度。它就是利用了上面我們說(shuō)的偏態(tài)分布中均值和中位數(shù)不相等來(lái)計(jì)算的。
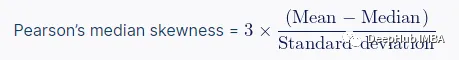
皮爾遜中位數(shù)偏度是計(jì)算均值和中位數(shù)之間有多少個(gè)標(biāo)準(zhǔn)差。
真實(shí)的觀測(cè)很少有剛好為0的皮爾遜偏中值。因?yàn)槿绻麛?shù)據(jù)的值接近于0,則可以認(rèn)為它具有零偏度,但是在實(shí)際數(shù)據(jù)中很少有沒(méi)有零偏度的分布數(shù)據(jù)。
例如,我們每年觀測(cè)到的太陽(yáng)黑子數(shù)量的Pearson中位數(shù)偏度:平均值= 48.6,中位數(shù)= 39,標(biāo)準(zhǔn)差= 39.5。那么公式如下:
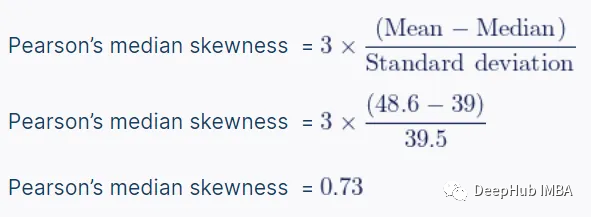
如果該值介于:
- -0.5和0.5,值的分布幾乎對(duì)稱(chēng)
- -1和-0.5之間為負(fù)偏斜,0.5到1之間為正偏斜。偏度適中。
- 如果偏度小于-1(負(fù)偏)或大于1(正偏),則數(shù)據(jù)是高度偏斜。
如何處理有偏度數(shù)據(jù)
如果你的統(tǒng)計(jì)過(guò)程需要正態(tài)分布并且你的數(shù)據(jù)是傾斜的,你通常有三個(gè)選擇:
- 什么也不做:許多統(tǒng)計(jì)檢驗(yàn),包括t檢驗(yàn)、方差分析和線性回歸,對(duì)偏斜數(shù)據(jù)不太敏感。特別是如果偏斜是輕微或中度的,最好的辦法就是忽略它。
- 數(shù)據(jù)轉(zhuǎn)換:通過(guò)對(duì)數(shù)據(jù)應(yīng)用某種變換,可以調(diào)整數(shù)據(jù)的分布形狀,使其更接近對(duì)稱(chēng)分布。常見(jiàn)的數(shù)據(jù)轉(zhuǎn)換方法包括取對(duì)數(shù)、開(kāi)方、平方根等。這些轉(zhuǎn)換可以減小或消除數(shù)據(jù)的偏度。
- 使用不同的模型:你可能想選擇一個(gè)不假設(shè)正態(tài)分布的模型,非參數(shù)測(cè)試或廣義線性模型可能更適合您的數(shù)據(jù)。比如說(shuō)非參數(shù)方法:如果數(shù)據(jù)的偏度較大,而且無(wú)法通過(guò)簡(jiǎn)單的轉(zhuǎn)換來(lái)糾正,可以考慮使用非參數(shù)統(tǒng)計(jì)方法。非參數(shù)方法不依賴(lài)于分布的假設(shè),而是直接對(duì)數(shù)據(jù)進(jìn)行分析,例如使用中位數(shù)作為代表性的位置測(cè)度,而不是平均值。
- 分組分析:如果數(shù)據(jù)集中存在明顯的子群體,可以考慮對(duì)數(shù)據(jù)進(jìn)行分組分析。通過(guò)將數(shù)據(jù)分成多個(gè)子群體,并對(duì)每個(gè)子群體進(jìn)行單獨(dú)的分析,可以更好地了解數(shù)據(jù)的特征和偏度情況。
- 針對(duì)特定問(wèn)題采取相應(yīng)的方法:根據(jù)具體的數(shù)據(jù)和分析目的,可以采用特定的方法來(lái)處理偏度數(shù)據(jù)。例如,在回歸分析中,可以使用偏度穩(wěn)定轉(zhuǎn)換(skewness-stabilizing transformation)來(lái)調(diào)整數(shù)據(jù)的偏度,以滿(mǎn)足回歸模型的假設(shè)。
下表總結(jié)了一些常用數(shù)據(jù)變換:

總結(jié)
數(shù)據(jù)的偏度是用來(lái)衡量概率分布或數(shù)據(jù)集中不對(duì)稱(chēng)程度的統(tǒng)計(jì)量。它描述了數(shù)據(jù)分布的尾部在平均值的哪一側(cè)更重或更長(zhǎng)。通過(guò)計(jì)算偏度,可以更好地了解數(shù)據(jù)的分布特征,并在需要時(shí)采取適當(dāng)?shù)臄?shù)據(jù)處理或分析方法。但是需要注意的是,偏度只是數(shù)據(jù)分布的一種度量,不能完全代表數(shù)據(jù)的整體特征,因此在分析數(shù)據(jù)時(shí)需要綜合考慮其他統(tǒng)計(jì)指標(biāo)和可視化方法。